1. 1自由度振動系のシミュレーション

公開日： 2014/11/10 基礎編

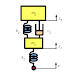
図1.1のようなモデルを1自由度振動系と呼ぶ。ここでの1自由度とは、質点 m がひとつであり、上下方向の運動のみを行うことを示している。
また、ばねとます(質点)とダンパで構成されているので、図1.1はばねますダンパ系とも呼ばれる。

ここでは、ばね下 z から上下方向の強制加振を行い、ばね上の周波数応答を、scilabとxcosを用いてシミュレーションする。

また、シミュレーション結果の妥当性を、ボード線図の結果と比較して検証をしたいと思う。

ｘcosでシミュレーションをする 

図1.1のモデルは、運動方程式(1.1)で表すことができる(1)。

各パラメータを表1.1に示す。

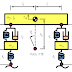
式(1.1)はブロック線図として、xcosで図1.2のように作成し、シミュレーションを行うことができる。入力は、ブロック線図の左にあるRead from input fileブロックから、ばね下 z の上下変位値を1ms刻みで行う。

ここでは、±0.024mの振幅の正弦波を、0.1Hzから20Hzに徐々に周波数を変化させたデータを用いた。

シミュレーションの結果、ばね上 x の時系列応答を図1.3 として出力することができる。

この出力グラフは、ばね上が300kg (車重でだいたい1200kg)、ばねレート3.0kgf/mmの車両が走行しているのと、同じような運動を実は表している。

Fig.1.3 強制加振ばね上応答

路面の凹凸が比較的ゆっくりしている場合には、車体は路面とほぼ同じ軌跡をたどる。しかし、凹凸の1周期が1秒間に1.39回(1.39Hz)まで速くなると、ばね上の車体が共振により、路面の凹凸よりも大きく揺れてしまうことが、グラフからわかる。
また、それ以上の速い入力に対しては、ばねとダンパが吸収をして、車体はあまり上下動をしなくなることも、グラフからわかる。

ちなみに共振の振幅のピーク値が、グラフから0.035mと読み取れるので、ゲインは
0.035m / 0.024m ＝ 1.46
となる。

ボード線図からも計算してみる

伝達関数からボード線図を求め、上記のシミュレーションの結果の妥当性を確認してみる。

ボード線図をもとめるには、運動方程式(1.1)をラプラス変換して、まず伝達関数(1.2)を求める(1)。

伝達関数をscilabに入力すると、図1.5のボード線図を出力することができる。
scilabへの入力コマンドは、図1.4とする(2)。

Fig. 1.4 ボード線図入力コマンド

Fig. 1.5 ボード線図出力結果

ボード線図から読み取れるピーク値3.3dBとなる。ボード線図のゲインは対数値を20倍した値なので、式(1.3)で元に戻してあげると(3)、

となり、シミュレーションと同じ1.46となることを確認できる。

共振周波数は1.37Hzで、シミュレーションの1.39Hzと若干ずれるが、グラフから読み取っているので、まあ良しとしてしまう。


◆参考文献 
　(1)自動車のサスペンション、カヤバ工業、pp. 107
　(2)橋本洋志、石井千春、小林裕之、大山恭弘共著、Scilabで学ぶシステム制御の基礎、オーム社
　(3)Wikipedia、フリー百科事典、ボード線図
◆使用アプリケーション
　scilab-xcos 5.3.3