4. セミアクティブ4自由度シミュレーション

公開日： 2015/09/15 応用編

1974年にKarnoppらの提唱した、スカイフック理論を近似したセミアクティブ制御モデル(1)をsilab-xcosで作成し、時系列のシミュレーションをしてみる。

シミュレーションはパッシブな油圧ダンパの代わりに、セミアクティブ制御力を加えた図4.1のモデルを用いる。

便宜的に入力点 z f と z r を路面、m1 f と m1 r をばね下、m 2 をばね上と呼ぶことにする。


4自由度のシミュレーションのパッシブモデルにも同じ入力を行い、2つのモデルの応答を比較することで、制御によるメリットとデメリットを検証してみたいと思う。

シミュレーションの結果をみてみる

シミュレーションの結果を、blenderの3Dモデルに入力して、ばね上とばね下の応答を観察する。シミュレーションの詳細については後述する。

向かって右側の車両がセミアクティブ制御モデルで、左側の車両がパッシブな油圧ダンパモデルである。

路面からの入力は、ここでは前後を同位相とした。

セミアクティブ制御モデルのばね下は、低周波数では良く動き、パッシブなモデルよりもばね上の上下動が早く収束する様子が観察できる。

ばね上とばね下の、変位と加速度は図4.2になる。

セミアクティブ制御の上下動が早く収束することは、ばね上の変位グラフの図4.2-2と、図4.2-1の違いからもわかる。

ばね上の加速度についても、図4.2-6から図4.2-5のように減少し、乗員がフワフワと感じるような固有振動を抑えることができ、これがセミアクティブ制御のメリットだといえると思う。

しかし、アニメーションの終盤では、ばね下のばたつきがみられる。

ばね下のばたつきによる乗り心地への影響は、ばね上の上下加速度の図4.2-5から、軽微だと推測されるが、振動を室内に騒音として伝える可能性がある。

また、ばね下の上下加速度の図4.2-7からは、ばたつき時の加速度が15m/s2を超えており、タイヤへの負担が大きくなることなどが懸念され、これは制御によるデメリットになると思う。

また、ばね上の加速度の図4.2-5には、低周波においても小刻みな振動がみられる。これはセミアクティブ制御のON/OFFのチャタリングによるもので、ばね下のばたつきと同様に、室内に振動を騒音として伝える原因になると思う。

逆位相の結果をみてみる

前後に逆位相の入力を行った場合には、以下のような応答を観察できる。

セミアクティブモデルは前後同位相のときと同様に、固有値付近のばね上の動きが抑えられていることがわかる。

逆位相のばね上のピッチ角とピッチ角速度は、以下のようになる。

路面入力について

路面からの入力は、±0.24mmの振幅の正弦波の周波数を、0.2～20Hzに徐々に変化させ、式4.1で表されるローパス特性の伝達関数フィルタを通して生成した(2)。

ここで、 w は周波数を変化させた正弦波の入力とし、ｚ は路面の入力とする。
また、ωd =2π、ζd =1とした。

走行速度を30km/hと仮定すると、路面のパワースペクトル密度は図4.3のようになった。ISO8608 (1995)に規定されている、H級付近に相当するので、かなりの悪路を低速で走行しているシミュレーションになると思う。

セミアクティブ制御の減衰比について

セミアクティブ制御モデルの減衰比は、前後共に1.2とした。

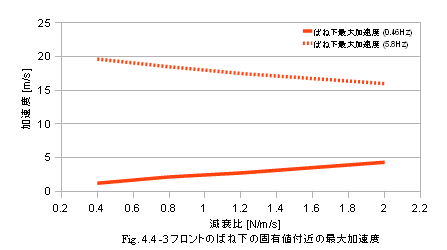
減衰比の違いによる影響をみるために、減衰比を0.4から2.0まで変化させ、フロントのばね上とばね下の、固有値の最大変位と最大加速度を調べてみたところ、以下の結果となった。

ばね上とばね下の固有値はそれぞれ0.46Hz、5.8Hzとしている。

減衰比が大きいほど、ばね上とばね下の最大変位は減少する傾向が、図4.4-1からわかる。

ただし、減衰比1.2を境にばね上の加速度は、悪化する傾向が図4.4-2にみられる。これは、制御のON/OFF切り替えにより生じる、ショックが増加したことが原因と考えられる。

ちなみに、通常の油圧ダンパを用いたパッシブモデルでも、減衰比をセミアクティブと同じ1.2にすれば、ばね上の固有振動はかなり抑えることができる。

しかし、その影響で乗り心地が相当に硬くなるし、セミアクティブのように固有値付近の上下変位のゲインが1を下回るようなことはないので、ここでは試していない。

各パラメータについて

セミアクティブモデルとパッシブモデルのパラメータは、基本的には4自由度のシミュレーションの値をそのまま使用した。ただし、前述のセミアクティブの制御に関わる、前後の減衰比は1.2として、減衰係数 csky f と csky r を算出した。

運動方程式とブロック線図

運動方程式についても、セミアクティブモデルとパッシブモデルは4自由度のシミュレーションの式3.2を使用している。
ただし、セミアクティブ制御モデルのcf と cr は以下の式4.2とする(3)。
式4.2はセミアクティブの制御のキモになる部分である。

式3.2と式4.2を合わせた運動方程式は、図4.5のブロック線図で表せると思う。

路面入力はブロック線図の左にある、Read from input fileブロックから、1ms 刻みで行う。前述のローパス特性の伝達関数ブロックを通し、zf と zr に上下変位値を渡す。

同位相と逆位相の切換えは、リアの路面入力 zr の直前に設置したゲインブロックの値を、1と-1にすることで行っている。

Fig 4.5 ブロック線図

ブロック線図のwrite to output fileで出力される、csvデータをblenderに入力すると、冒頭のアニメーションを作成することができる。

スカイフック近似セミアクティブ制御は、制御方法がシンプルで、Gセンサと電磁バルブのみで、フルアクティブに近い制御を実現できる方法である(1)。しかし、ばね下のばたつきや、制御にチャタリングが発生しやすいので、実用化には課題が多そうだ。



◆参考文献
　(1)Karnopp, D., Crosby, M. J. and Harwood, R. A., Vibration Control Using Semi-Active Force Generators, Transactions of the ASME, Journal of Engineering for industory, (1974)
　(2)姜 聲国, 吉田和夫, H∞制御理論によるフィードフォワード併合振動絶縁制御, 日本機会学会論文集C編, Vol. 58, No.556, (1992)
　(3)岡本文太, 吉田和夫, 自動車用セミアクティブサスの外乱包含双線系最適制御, 日本機会学会論文集C編, Vol.66, No.650, (2000)
◆使用アプリケーションおよびモデル
　simulation: scilab 5.3.3
　model: sketchup 2014
　(vehicle model: mandun)
　export obj (plugin): obj_in-out (Akitenh)
　rendering: blender 2.57
　csv import: phyton 2.7.7, csv f-curve importer v7.0 alpha1
　fft: fftexc 2.0