5. イナータ3自由度シミュレーション
公開日: 2015/10/25 基礎編
 |
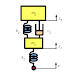
| Fig. 5.1 Inerter 3DOF model |
イナータは、2005年のF1サンマリノグランプリで、マクラーレンが初めて実戦に投入した(1)、比較的新しいサスペンションのデバイスである。
 |
| Photo by ph-stop |
イナータは、ばね上の慣性質量を増加するのに似た効果があり、不必要なタイヤの振動を抑え、グリップを向上させるといわれるが(2)(3)、具体的にどのような働きをするのかとてもかわかりにくい。
そこでまず、考案者のMalcolm Smithが提案したいくつかのクォータモデル(4)のうち、図5.1の3自由度モデルのシミュレーションを行うことにより、その効果の一端を探ってみようと思う。
ここでは、入力に対するばね上変位のボード線図を作成し、通常の油圧ダンパモデルと比較しながら、イナータの効果を最も得られるようなセッティングを探してみたいと思う。
便宜的に図5.1の m3 をばね上、m1 をばね下、k4 をメインスプリング、k3 をイナータスプリング、k2 をダンパスプリングと呼ぶことにする。
モデルのパラメータ j で表される部分をイナータとし、質量 m2 は簡略化のためにゼロとする。
イナータは、はずみ車とそれを回転させる機構で構成される。
ここでは図5.2のような、ボールねじを用いた機構でシミュレーションを行う。
Malcolm Smithは、はずみ車を回転させる機構に、ラックアンドピニオンと歯車を採用していたが(4)、直動を回転に変える比率が同じであれば、結果に差異はないと思う。
イナータの運動方程式は、式5.1で表される(5)。
I ははずみ車の慣性モーメント、θ'' ははずみ車の角加速度、d はボールねじの外径、p はボールねじのピッチ、F j はデバイスへの入力とする。
式5.1を F j について整理すると、式5.2になる。
式5.2からイナータは、入力の加速度 (x''2 - x''3)に比例して、力を発生することがわかる。
また、はずみ車の慣性モーメント I が増加しても、それに比例して力が増加する。ボールねじピッチ p が減少した場合には、はずみ車の回転速度が増加して、その2乗に比例して力が増加することもわかる。
なお、力の伝達に関わる抵抗力や、部品同士の隙間は十分に小さいものとして、ここでは考慮しない。
車両モデルはLe Mans 24 Hoursなどの耐久レースを走行する、LMP1クラスを想定した。
ばねレートが低いと、イナータの効果が出にくいからだ。
F1をモデルにしなかったのは、サスペンションアームの動き3Dでつくるのが大変だったからである。
LMP1クラスの車両について、公開されている情報はほとんどないので、シミュレーションの結果と実車に関わりはなく、あくまでイナータの傾向をみる程度と考える。
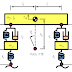
手前の車両がイナータモデルで、奥の車両が通常の油圧ダンパモデルとしている。
通常のダンパとの違いがわかりやすいように、上下動の振幅を大きくしてみたが、アニメーションからわかるのは固有振動の発生がすこし早い(周波数がすこしひくい)かなという程度だった。そこで、以下のグラフから違いを読み取ってみる。
ばね上の時系列の上下変位は図5.3-1と図5.3-2になり、グラフからイナータは、ばね上の固有振動を抑えていることがわかる。また、ピークの周波数が低くなることもわかる。
モデルのパラメータ j で表される部分をイナータとし、質量 m2 は簡略化のためにゼロとする。
イナータの構造と運動方程式
イナータは、はずみ車とそれを回転させる機構で構成される。
 |
| Fig.5.2 Inerter model |
ここでは図5.2のような、ボールねじを用いた機構でシミュレーションを行う。
Malcolm Smithは、はずみ車を回転させる機構に、ラックアンドピニオンと歯車を採用していたが(4)、直動を回転に変える比率が同じであれば、結果に差異はないと思う。
イナータの運動方程式は、式5.1で表される(5)。
I ははずみ車の慣性モーメント、θ'' ははずみ車の角加速度、d はボールねじの外径、p はボールねじのピッチ、F j はデバイスへの入力とする。
式5.1を F j について整理すると、式5.2になる。
式5.2からイナータは、入力の加速度 (x''2 - x''3)に比例して、力を発生することがわかる。
また、はずみ車の慣性モーメント I が増加しても、それに比例して力が増加する。ボールねじピッチ p が減少した場合には、はずみ車の回転速度が増加して、その2乗に比例して力が増加することもわかる。
なお、力の伝達に関わる抵抗力や、部品同士の隙間は十分に小さいものとして、ここでは考慮しない。
シミュレーション結果をみてみる
車両モデルはLe Mans 24 Hoursなどの耐久レースを走行する、LMP1クラスを想定した。
ばねレートが低いと、イナータの効果が出にくいからだ。
F1をモデルにしなかったのは、サスペンションアームの動き3Dでつくるのが大変だったからである。
LMP1クラスの車両について、公開されている情報はほとんどないので、シミュレーションの結果と実車に関わりはなく、あくまでイナータの傾向をみる程度と考える。
手前の車両がイナータモデルで、奥の車両が通常の油圧ダンパモデルとしている。
通常のダンパとの違いがわかりやすいように、上下動の振幅を大きくしてみたが、アニメーションからわかるのは固有振動の発生がすこし早い(周波数がすこしひくい)かなという程度だった。そこで、以下のグラフから違いを読み取ってみる。
ばね上の時系列の上下変位は図5.3-1と図5.3-2になり、グラフからイナータは、ばね上の固有振動を抑えていることがわかる。また、ピークの周波数が低くなることもわかる。
 |
| Fig.5.3-1 Ineter model displacement |
 |
| Fig.5.3-2 Conventional model displacement |
図5.4-1と図5.4-2からは、タイヤと路面の荷重変化も抑えられることがわかるので、タイヤのグリップも向上すると考えられる。
 |
| Fig.5.4-1 Ineter model load on tire |
 |
| Fig.5.4-2 Conventional model load on tire |
各パラメータについて
LMP1クラスの車両に比較的近いと思われる、F1のばねの固有振動数は、5Hzから7Hzといわれているようなので(6)、固有振動数は6Hzとした。
900kgf前後の車重以外に、公開されているデータはみつからなかったので、ここでは近しいと考えられる、表5.1の値を使用した。
以降は、イナータの効果が最大となる、k2、k3、j を求める作業を行う。
運動方程式から伝達関数を求める
まず、伝達関数を求めるために、運動方程式を作成する。
図5.1のモデルの、運動方程式は式5.3で表される。
式5.3を m2=0 として、x''3 と x''2 、x''1 について整理すると、式5.4になる。
式5.4をラプラス変換して、ばね上の伝達関数 x3 / z を求めると、式5.5になる。
式5.5の伝達関数を求める計算は、すごく手間なので、今回はフリーウェアのmaximaを利用した。
maximaでは文字の含まれる数式を、数式のまま解くときに、とても便利である(7)。
数式に数値を代入する計算には、これまで通りscilabを使う。
maximaへのコマンドは以下とした。
 |
| Fig.5.3 maxima command |
コマンドの5行目の f5 では、式5.3をラプラス変換した方程式 [f1, f2, f3, f4] の、[x1, x2, x3, p] についての解を求めている。6行目の fullratsimp で f5 を整理して式5.5を求めた。
伝達関数からボード線図を作成する
式5.5の伝達関数からscilabを用いて、ボード線図を作成し、ばね上のゲイン x3 / z の周波数応答を求める。
最適なパラメータを得るために、ダンパスプリングのばねレート k2 を、まず変化させてみる。
k2 の値を0~500N/mmに変化させると、ボード線図は図5.5となった。
その他のパラメータは暫定で、k3=300N/mm、j=1500kg とした。
 |
| Fig.5.5 k2=0-500[N/mm], k3=300[N/mm], j=1500[kg] |
ダンパスプリングのレートが小さくなると、通常の油圧ダンパモデルの特性に近づいていき、100N/mm以下では振動のピークが油圧ダンパモデルを下回り、0N/mmがもっともゲインが小さくなる。
そこで、ダンパスプリングのばねレート k2 を0N/mmに固定して、今度はイナータスプリングのばねレート k3 を0~500N/mmに変化させて、ボード線図にしてみる。
イナータのパラメータ j は1500kgのままである。
 |
| Fig.5.6 k2=0[N/mm], k3=0-500[N/mm], j=1500[kg] |
イナータスプリングのレートが100N/mm付近では4Hz以下の振動の増加が少なく、4.7Hzのピークを抑えられることがわかる。
そこで、イナータスプリングのばねレート k3 を100N/mmに固定して、最後にイナータのパラメータ j を500~4500kgに変化させる。
 |
| Fig.5.7 k2=0[N/mm], k3=100[N/mm], j=500-4500[kg] |
イナータのパラメータ j が大きくなると、通常の油圧ダンパモデルの特性に近づく。パラメータ j が900kg付近で振動のピークが最も小さくなり、それ以下では逆に4Hz以下の振動のピークが大きくなる。
結論として
今回の条件では k2=0N/mm(スプリング無し)、k3=100N/mm、j=900kg が、最もピーク振動を抑えられると考えられる。
そのボード線図は図5.8となる。
 |
| Fig.5.8 k2=0[N/mm], k3=100[N/mm], j=900[kg] |
今回はパラメータが多いので、メインスプリングのばねレート k4 とタイヤのばねレート k1 、ダンパの減衰係数 c については、比較する通常のパッシブダンパと同じ値で固定している。
ばねレートを小さくしてしまうと、低周波のばね下の固有振動は減少するが、それはイナータの効果ではなく、ロール剛性も小さくなり、走行性能も変化してしまうからである。
入力について
入力はセミアクティブのシミュレーションと同じものを使用した。
ブロック線図について
式5.4の運動方程式をブロック線図にすると、図5.9になる。
ブロック線図のwrite to output fileで出力される、csvデータをblenderに入力すると、冒頭のアニメーションを作成することができる。
クォータモデルのシミュレーションであることから、ここでは各輪の入力および、応答は同じものとしている。
F1の車両でイナータが実際に採用されているのは、ヒーブダンパと同様のレイアウトである(8)。
ヒーブダンパは、サードダンパとも呼ばれる、左右のタイヤが同位相で動いたときに、ストロークするダンパである。
ヒーブダンパと同様のシミュレーションは、モデルがより複雑になり、影響を与えるパラメータも多く、評価が複雑になることが予想される。そこで、ここではまず基本的な特性を把握するために、シンプルなクォータモデルを用いた。
今回のクォータモデルからわかることは、イナータのフライホイールの質量には適切な値があり、それを調整することで、ばね上の振動のピークを抑え、周波数を下げられることである。
それと同時に、タイヤと路面の荷重変化を抑えられるので、タイヤのグリップが増加すると考えられる。
路面の上下振幅については、アニメーションで動きがわかりやすいように、これまでと同じ±0.24mとしている。その振幅ではタイヤが路面から離れてしまうことが、タイヤと路面の荷重グラフからわかると思う。
ただし、振幅が小さくても結果は同じということで、ここではよしとしてしまう。
時間があれば、F1と同じレイアウトでも試してみたい。
◆参考文献
(1)Wikipedia, the free encyclopedia, Inerter
(2)F1Technical.net, J-dampers in Formula 1
(3)Racecar enginiering, J damper in Formula 1
(4)Malcolm C. Smith, The Inerter Concept and Its Application, Sosiety of Instrument and Control Engineers (SICE) Annual Conference, Fukui, Japan, (2003)
(5)富樫研究開発, ダンパー講座, 96.Inerter
(6)富樫研究開発, ダンパー講座, 84.Natural Frequency
(7)川谷亮治, フリーソフトで学ぶ線形制御 Maxima/Silab活用法, 森北出版株式会社
(8)Racecar enginiering, F1 2014 explained: What is FRICS?
 |
| Fig.5.9 Inerter block model |
ブロック線図のwrite to output fileで出力される、csvデータをblenderに入力すると、冒頭のアニメーションを作成することができる。
クォータモデルのシミュレーションであることから、ここでは各輪の入力および、応答は同じものとしている。
考察してみる
F1の車両でイナータが実際に採用されているのは、ヒーブダンパと同様のレイアウトである(8)。
ヒーブダンパは、サードダンパとも呼ばれる、左右のタイヤが同位相で動いたときに、ストロークするダンパである。
ヒーブダンパと同様のシミュレーションは、モデルがより複雑になり、影響を与えるパラメータも多く、評価が複雑になることが予想される。そこで、ここではまず基本的な特性を把握するために、シンプルなクォータモデルを用いた。
今回のクォータモデルからわかることは、イナータのフライホイールの質量には適切な値があり、それを調整することで、ばね上の振動のピークを抑え、周波数を下げられることである。
それと同時に、タイヤと路面の荷重変化を抑えられるので、タイヤのグリップが増加すると考えられる。
路面の上下振幅については、アニメーションで動きがわかりやすいように、これまでと同じ±0.24mとしている。その振幅ではタイヤが路面から離れてしまうことが、タイヤと路面の荷重グラフからわかると思う。
ただし、振幅が小さくても結果は同じということで、ここではよしとしてしまう。
時間があれば、F1と同じレイアウトでも試してみたい。
◆参考文献
(1)Wikipedia, the free encyclopedia, Inerter
(2)F1Technical.net, J-dampers in Formula 1
(3)Racecar enginiering, J damper in Formula 1
(4)Malcolm C. Smith, The Inerter Concept and Its Application, Sosiety of Instrument and Control Engineers (SICE) Annual Conference, Fukui, Japan, (2003)
(5)富樫研究開発, ダンパー講座, 96.Inerter
(6)富樫研究開発, ダンパー講座, 84.Natural Frequency
(7)川谷亮治, フリーソフトで学ぶ線形制御 Maxima/Silab活用法, 森北出版株式会社
(8)Racecar enginiering, F1 2014 explained: What is FRICS?
◆使用アプリケーションおよびモデル
simulation: scilab 5.3.3
model: sketchup 2014
(vehicle model: Tatsuki.S)
export obj (plugin): obj_in-out (Akitenh)
rendering: blender 2.57
csv import: phyton 2.7.7, csv f-curve importer v7.0 alpha1
equation solver: maxima 5.37.2