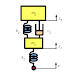
6.状態方程式の2自由度シミュレーション
公開日: 2016/05/06 基礎編
 |
| Fig 6.1 Continuous state-space system block diagram |
Scilab/XcosのCLSSブロックを用いて、2自由度振動系のシミュレーションをしてみる。
CLSSブロックは状態方程式の計算を行うブロックである。
状態方程式はこれまで力のつり合いから作成してきたような、運動方程式から導き出すことができる。
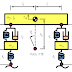
CLSSブロックに状態方程式を定義することで、図6.1のようなブロックひとつで、これまでの図2.2の運動方程式の計算と同じことがができる。
 |
| Fig 2.2 Equation of motion block diagram |
ここでは、運動方程式から状態方程式を導き出し、CLSSブロックを用いてシミュレーションを行い、運動方程式のシミュレーション結果と比較して、計算に誤りがないか検証してみたいと思う。
運動方程式から状態方程式をつくる
 |
| Fig 2.1 2 DOF model |
対象の運動モデルは、2自由度のシミュレーションの図2.1を用いる。力のつり合いから運動方程式は式(2.1)となる。
まず運動方程式から状態方程式を導き出す。
これを状態方程式の一般形の式(6.1)の形に導く。
ここで、u は入力であり、 y は出力である。
今回はばね上の変位と、ばね下の変位を出力したいので、 x 、 x' 、 u 、y を、式(6.2)のように設定すると、
これをコンテキスト設定に以下のように記述し、
//車両諸元
m1=30; //ばね下重量[kg]
m2=300; //ばね上重量[kg]
c2=3000; //ダンパー減衰比[N/m/s]
k2=30000; //ばね定数[N/m]
k1=300000; //タイヤばね定数[N/m]
//状態方程式の定数行列
A=[0 1 0 0;-(k1+k2)/m1 -c2/m1 k2/m1 c2/m1;
0 0 0 1;k2/m2 c2/m2 -k2/m2 -c2/m2]; //システム行列
B=[0;k1/m1;0;0]; //入力行列
C=[1 0 0 0;0 0 1 0]; //出力行列
ブロックパラメータには図6.2のように設定することで、シミュレーションを行う。
 |
| Fig 6.2 Continuous state-space system parameters |
入力について
路面 z からの入力は、2自由度のシミュレーションと同じものを用いた。
結果を比較してみる
図6.1と図2.2のブロック線図を結合してシミュレーションを行うと、図6.3のように出力グラフが完全に重なることを確認できた。(CLSSブロックからの出力でグラフが上書きされている)
 |
| Fig 6.3 Displacement graph (overwritten with CLSS graph) |
CLSSブロックを使ってみて
シミュレーションにかかる時間が、これまでの運動方程式のブロック線図より早くなることを、実は期待していたが、計算時間は同じだった。
また、CLSSブロックは線形モデルしか記述できないようなので、非線形モデルを扱うには、近似式を導くことになる。特別に必要がなければこれまで通り、運動方程式のブロック線図を使っても、支障はないのではと感じる。
ただし、現代制御理論では対象となるモデルを状態方程式で表現するので(2)、ロバスト制御などの複雑な制御を行う際には、CLSSブロックを使う必要がでてくるだろうと思う。
◆参考文献
(1)吉田和信,現代制御理論ノート2000年度後期(制御工学III), 島根大学総合理工学部電子制御システム工学科
(2)橋本洋志, 石井千春, Scilab/Scicosで学ぶシミュレーションの基礎, オーム社
◆使用アプリケーションおよびモデル
Simulation: Scilab 5.5.2